CryptoSystem — TryHackMe Walkthrough

Last updated: July 17, 2025

In this crypto challenge, we have been given an RSA-encrypted message, and we have to find the key

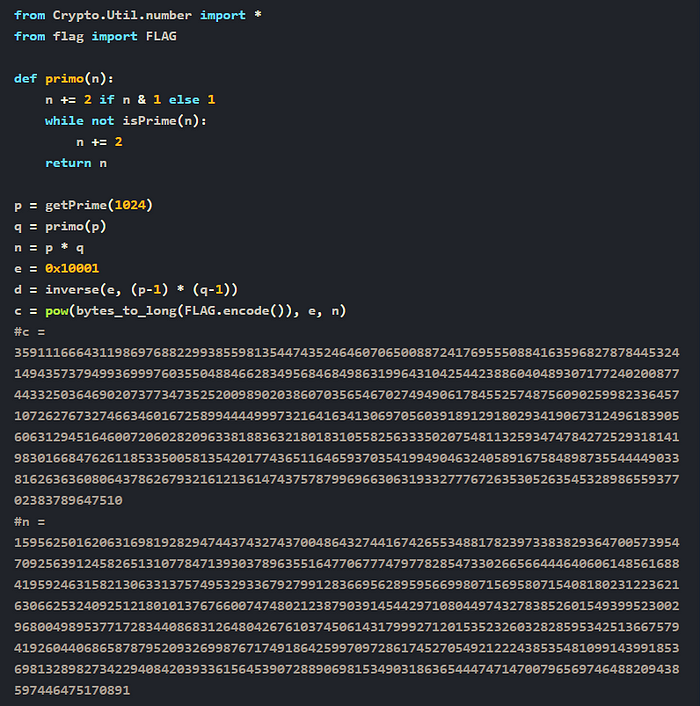
We were presented with a Python script that implemented a custom RSA encryption scheme. The script generated two large prime numbers: p, using the getPrime() function to create a 1024-bit prime, and q, using a custom function called primo(p), which finds the next prime number after p. This is highly unusual and insecure because p and q are normally selected to be large and random, but also distant from each other to make factoring n = p * q hard.

In our case, since q was derived directly from p as q = next_prime(p)It introduced a serious vulnerability — the two primes were very close to one another, which made factoring n feasible using a simple brute-force approach.

Below is a Python script to brute-force nearby primes around the square root of n and successfully factor it. After recovering the private key, the script decrypts the ciphertext and Displays the flag.

Decryption Script:

OR Download from GitHub

from Crypto.Util.number import *
from sympy import isprime, nextprime
import math

c = 3591116664311986976882299385598135447435246460706500887241769555088416359682787844532414943573794993699976035504884662834956846849863199643104254423886040489307177240200877443325036469020737734735252009890203860703565467027494906178455257487560902599823364571072627673274663460167258994444999732164163413069705603918912918029341906731249618390560631294516460072060282096338188363218018310558256333502075481132593474784272529318141983016684762611853350058135420177436511646593703541994904632405891675848987355444490338162636360806437862679321612136147437578799696630631933277767263530526354532898655937702383789647510

n = 15956250162063169819282947443743274370048643274416742655348817823973383829364700573954709256391245826513107784713930378963551647706777479778285473302665664446406061485616884195924631582130633137574953293367927991283669562895956699807156958071540818023122362163066253240925121801013767660074748021238790391454429710804497432783852601549399523002968004989537717283440868312648042676103745061431799927120153523260328285953425136675794192604406865878795209326998767174918642599709728617452705492122243853548109914399185369813289827342294084203933615645390728890698153490318636544474714700796569746488209438597446475170891

e = 0x10001

def factor_n(n):
    approx_p = int(math.isqrt(n))
    if approx_p % 2 == 0:
        approx_p -= 1

    for i in range(10000):  
        p = approx_p - i
        if isprime(p):
            q = nextprime(p)
            if p * q == n:
                return p, q
    return None, None

p, q = factor_n(n)
if p is None:
    print("Failed to factor n")
    exit()

phi = (p - 1) * (q - 1)
d = inverse(e, phi)

m = pow(c, d, n)
plaintext = long_to_bytes(m)
print(f"[+] Recovered FLAG: {plaintext.decode()}")

NOTE: Before running it, we have to start a virtual environment and install some libraries:

So, first, we will set up the virtual environment

python3 -m venv ~/python

source ~/python/bin/activate

And then we will install some required Libraries:

pip3 install pycryptodome

pip3 install sympy

And now run the script

Too easy 🙂